Física.: Clase 2.

Lanzamiento Parabólico Completo.

Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme.

Puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical.

1. La independencia de la masa en la caída libre y el lanzamiento vertical es igual de válida en los movimientos parabólicos.

2. Un cuerpo lanzado verticalmente hacia arriba y otro parabólicamente completo que alcance la misma altura tarda lo mismo en caer.

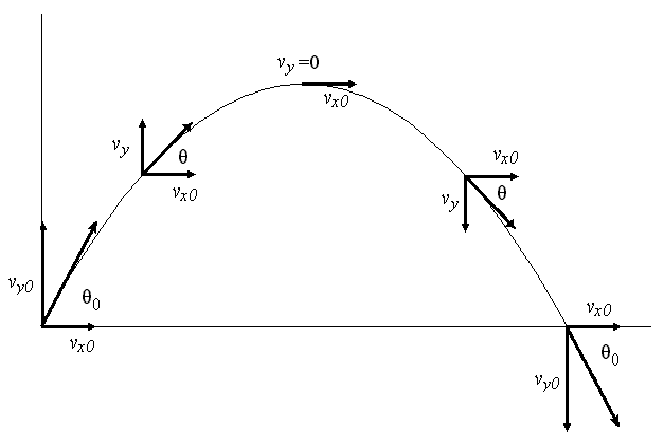
Para facilitar el estudio del movimiento de un proyectil, frecuentemente este se descompone en las direcciones horizontal y vertical. En la dirección horizontal el movimiento del proyectil es rectilíneo y uniforme ya que en esa dirección la acción de la gravedad es nula y consecuente, la aceleración también lo es. En la dirección vertical, sobre el proyectil actúa la fuerza de gravedad que hace que el movimiento sea rectilíneo uniformemente acelerado, con aceleración constante.

se hará uso de las siguientes formulas para este movimiento:

$a_{x}=0$    $v_{x}=v_{0}cos(\theta )$ $x=v_{0}cos(\theta )t$
$a_{y}=-g$ $v_{y}=v_{0}sen(\theta )-gt$    $y=v_{0}sen(\theta )t-\frac{1}{2}gt^2$

Y a estas dos ecuaciones las llamamos ecuaciones paramétricas de la trayectoria:
$x=v_{0}cos(\theta )t$    $y=v_{0}sen(\theta )t-\frac{1}{2}gt^2$
y si despejamos t de la primera ecuación obtenemos la función:
$y = xtan(\theta )-\frac{gx^2}{2v_{0}^2cos^{2}(\theta )}$
Que efectivamente no es mas que una parábola.

Alcance.

El alcance horizontal de cada uno de los proyectiles se obtiene para y=0.

$x_{max}=\frac{v_{0}^{2}sen(2\theta )}{g}$

Su valor máximo se obtiene para un ángulo θ = 45º, teniendo el mismo valor para θ = 45 + a , que para θ = 45 - a. Por ejemplo, tienen el mismo alcance los proyectiles disparados con ángulos de tiro de 30º y 60º, ya que sen(2·30°) = sen(2·60°).
Altura Máxima.
La altura máxima que alcanza un proyectil se obtiene con vy = 0.
$y_{max}=\frac{v_{0}^{2}sen^{2}(\theta )}{2g}$
Su mayor se obtiene cuando se dispara con un angulo θ = 90º .
Tiempo de Vuelo.
El tiempo en el que el proyectil pasara en el aire se obtiene cuando y = 0 esta dado por la formula.
$t_{vuelo}=\frac{2v_{0}sen(\theta )}{g}$
Donde se alcanza el máximo cuando se dispara con un angulo θ = 90º.

Ejemplos:

1- Calcular el alcance, la altura máxima y el tiempo de vuelo de un lanzamiento parabólico completo

que tiene una velocidad inicial de 30mt/s y un angulo de partida de 60° con respecto a la horizontal.

Solución:

Primero calcularemos el alcance.

$x_{max}=\frac{v_{0}^2sen(2\theta )}{g}=\frac{(30\frac{mt}{s})^2sen(2(60^{\circ}))}{9.8\frac{mt}{s^2}}=79.53mt$

La altura máxima sera:
$y_{max}= \frac{v_{0}^2sen^2(\theta )}{2g}=\frac{(30\frac{mt}{s})^2sen^2(60^{\circ})}{2(9.8\frac{mt}{s^2})}=34.43mt$
El tiempo de vuelo sera:
$t_{vuelo}=\frac{2v_{0}sen(\theta )}{g}=\frac{2(30\frac{mt}{s}sen(60^{\circ}))}{9.8\frac{mt}{s^2}}=5.3s$

Lanzamiento de Media Parábola.

El movimiento de media parábola o semiparabólico (lanzamiento horizontal) se puede considerar como la composición de un avance horizontal rectilíneo uniforme y la caída libre, tiene la característica que:

Un cuerpo que se deja caer libremente y otro que es lanzado horizontalmente desde la misma altura tardan lo mismo en llegar al suelo.

Las ecuaciones de este movimiento son:
$a_{x}=0$ $v_{x}=v_{0}$ $x=v_{0}t$
$a_{y}=g$ $v_{y}=gt$ $y=\frac{1}{2}gt^2$

Lanzamiento Parabólico con Altura Inicial.

Se dispara un proyectil desde una altura h sobre un plano horizontal con velocidad inicial v0, haciendo un ángulo θ con la horizontal. Para describir el movimiento establecemos un sistema de referencia como se indica en la figura.

Las componentes de la velocidad del proyectil en función del tiempo son: